TImageEnProc.WallisFilter

Declaration

procedure WallisFilter(WinWidth: Integer = 2; WinHeight: Integer = 2; Mean: Integer = 50; StDev: Integer = 50; InGain: Integer = 50; Edge: Integer = 10; Limit: Integer = 50; Thresholding: Boolean = False);

Description

Apply a Wallis Filter to the image. The Wallis Filter is a locally adaptive image enhancement algorithm.

Parameter	Description
WinWidth/WinHeight	Dimensions of the window as a percentage of the image size (e.g. 2 is a window size 2% of the width/height)
Mean	Specifies the local mean. Range: 0-100. Typical value is 50
StDev	Specifies the local standard deviation (contrast) of the output. Range: 0-100. Commonly used range: 50-75
InGain	Controls the ratio of measured to desired local variance. Range: 0-infinity. If 0 there is no variance equalization
Edge	Controls amount of mean equalization. Range: 0-100. 100 is full mean equalization. 0 is measured mean restored
Limit	Specifies a limit for the correction
Thresholding	If true, pixels are set either white or black

Note:
◼A UI for this is available to your users in the Image Processing dialog
◼If the image PixelFormat is not ie24RGB, it will be converted

Demo

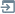Demos\ImageEditing\EveryMethod\EveryMethod.dpr

Comparison of Auto-Enhancement Methods

// Load test image
ImageEnView1.IO.LoadFromFile( 'D:\TestImage.jpg' );

// Apply a Wallis Filter to the image
ImageEnView1.Proc.WallisFilter();

// Improve the contrast and colors in the image
ImageEnView1.Proc.AutoImageEnhance1();

// Use a "Retinex" algorithm to simulate how humans see the world
ImageEnView1.Proc.AutoImageEnhance2();

// Enhance luminosity by applying a local adaptation tone mapping algorithm
ImageEnView1.Proc.AutoImageEnhance3();

Attribution

Wallis Filter is a locally adaptive image enhancement based on:
Wallis, R. An approach to the space variant restoration and enhancement of images.
Proceedings, Symposium on Current Mathematical Problems in Image Science, Monterey CA, 1976 10-12 reprinted in C.O. Wilde E. Barrett, eds. Image Science Mathematics, Western Periodicals, North Hollywood, CA, 1977.

Summarised in Pratt:
Pratt, W.K. Digital Image Processing, 2nd. ed. John Wiley & Sons, New York, 1991, 248, 503

Programming for Delphi:

I. Scollar 2003

  W A L L I S - STATISTICAL DIFFERENCING USING WALLIS ALGORITHM

  PURPOSE:

  IMPLEMENT THE STATISTICAL DIFFERENCING FILTER OF WALLIS (SEE
  W. PRATT, DIGITAL IMAGE PROCESSING) FOR LARGE PICTURES
  AND LARGE WINDOWS GREATER THAN 20X20

  EFFICIENT SAMPLING TECHNIQUE TO COMPUTE LOCAL MEANS AND VARIANCES.

  OPERATION:

  THE WINDOW DIMENSIONS AND 5 PARAMETERS FOR THE WALLIS FORMULA:
  MEAN DESIRED LOCAL MEAN OF OUTPUT A COMMONLY USED VALUE FOR MANY APPLICATIONS IS 128.ALLOWED RANGE 0-255.
  S.D. DESIRED LOCAL STANDARD DEVIATION (CONTRAST) OF OUTPUT PICTURE. ALLOWED RANGE 0-100. COMMONLY USED RANGE 50-75.
  GAIN CONTROLS RATIO OF MEASURED TO DESIRED LOCAL VARIANCE. ALLOWED RANGE 0-INFINITY
        EFFECT:
        0 NO VARIANCE EQUALIZATION
           THIS IS THE SAME AS LEE'S ALGORITHM (IEEE PROC. PRIP 1978,P.56)

        INF MAXIMUM VARIANCE EQUALIZATION
             THIS IS EQUIVALENT TO WATKIN'S ALGORITHM.
        COMMONLY USED RANGE 4-25.
  EDGE FACT. CONTROLS AMOUNT OF MEAN EQUALIZATION
        ALLOWED RANGE 0-1.
        EFFECT:
        100 FULL MEAN EQUALIZATION
        0 MEASURED MEAN RESTORED

  AUTHORS:

  B. WEIDNER, RLMB, 1979
  BASED ON IDEAS TAKEN FROM MVEQN/F BY I. SCOLLAR 1979
  BASED ON IDEAS TAKEN FROM ANAY14 BY G. TANG, 1977

TImageEnProc.WallisFilter